Precision and Accuracy: Changes to the Aiming System in 8.6

This post was supposed to come out a while ago, but with WoT NA servers down at the moment and the continuing arguments over just how 8.6 effected accuracy, I wanted to take some time to show you just what changed.

In 8.6, the aiming mechanism's RNG was changed to produce a tighter shot distribution. The details of this have been gone over multiple times, particularly in WG's own announcement and this article on ftr-wot.blogspot.cz  (blog now located at ftr.wot-news.com).

The gist of it simple pretty simple: Where once the outside of the aim circle represented 1.3 standard deviations from the aim point and any number >1.3 SDs generated by the RNG flew off to edge of the aim circle, this was being tweaked to be 3 standard deviations instead. Now that the patch is out, I'm fairly certain that the aim circle is still at 1.3-2 SDs in size as it appears smaller than it used to, but now the RNG will allow shots out to 3 SDs, which is the new definition of the gun's accuracy stat.

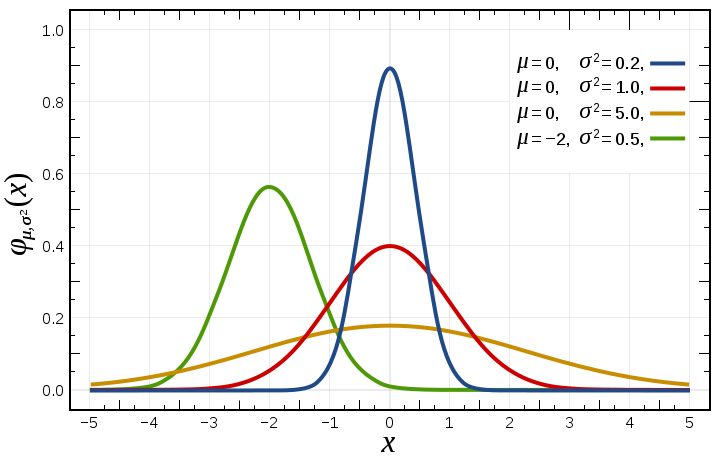
What does this mean practically? Well, take a look at a standard normal distribution:

The numbers along the bottom are distances in Standard Deviations and from the chart you can see that 68% of your shots will land within 1 SD of the aim point, 95% within 2 SDs and 99.7% within 3 SDs. For reasons unknown to players and statisticians the world around (programmers likely have a theory about system resources), Wargaming decided to set a hard limit on their random number generator at 1.3 SDs, which coincidently means that 1 in every 5 shots went straight to the edge of your aiming circle. By changing this value to 3 SDs, now only 3 in 1000 shots land directly on the edge of the aim circle. But that's not the only effect. The change "squeezes" the distribution, concentrating the shots towards the middle of the aim circle as can be seen by comparing the 8.5 (Red) and 8.6 (Blue) distributions in the image below:

Red represents, effectively, 8.5, and Blue represents 8.6. The wiki saves me the trouble of making an image again!

Now, it's all well and good to show you in the abstract what will change, but that's not how we experience shooting in game. Fortunately, someone already beat me to this part and made a couple of images illustrating how we can expect to see a set of individual shots:

Taifuuni's illustration of the change in shot distribution

So basically, more of your shots are going to be near the center of the circle, more closely concentrated at your point of aim. I would expect that everyone's first response is "Guns guns are getting more accurate!" Unfortunately, at this point I must put on my pendant pants. In my engineering education, someone put me through a big discussion on the difference between precision and accuracy and it stuck.

Guns in WoT have always been perfectly accurate. What they are not, however, is precise. Shots always average hitting the aim point. However, they do not always hit the target, rather they disperse over a rather large area. What this change will do is make all the guns in the game more precise as they will hit closer to center of the aim point.

Now, just how much more precise are we getting?

To measure precision, we probably want to compute something that tells us how far from the aim point we hit. I am going to use the average miss distance as our measure of precision, since direction doesn't change anything. That means (since we're only dealing with distances from the aim point) that our distribution is the half-normal distribution, the absolute value of a normal distribution.

The wiki says that gun accuracy is a 2 SD measure, but the FTR article suggests that shots will only deviate up to 1.3. I suspect that both may be right in that their way, so that while tanks have an accuracy given as the 2 SD measure, shots will never miss by that much.

Calculating it out, in 8.5, the average shot misses by 0.707 Standard Deviations, while those in 8.6 will miss, on average, by 0.79712 Standard Deviations. But I thought our guns were getting more precise?

They are, but not due to the change in the RNG. The precision is coming from the change in the definition of the Accuracy stat: Where once it was 2 SDs, it is now 3 SDs. So each Standard Deviation is 2/3rds the size of the old ones. Net Result is more precision. How much more?

Changes in the hit probability of the feared 183mm gun. Don't worry, it still hurts just as much.

It could be considered equivalent to giving everyone a 33% buff to accuracy along with the bonus of dealing with fewer shots hitting the edges of the circle. Except they didn't buff everyone, now did they?

One of the things WG said they wanted to do was leave the accuracy of artillery mostly unaffected. To do this they nerfed most artillery's accuracy value by 50%, which happens to just leave artillery with the same Standard Deviations as before.

The 261's 180mm gun will still hit just as often, it'll just miss by more when it misses.

Except that I just showed above that tanks will end up hitting further away, standard deviation wise, than before. Thus the change in the RNG is, in some ways, a nerf to Artillery, about 12%. Each shot will, on average, hit 12.7% further away from the Aim Point than before.

Summary:

1. All non-artillery pieces will have improved hit probability and miss their aim-point by smaller distances
2. Non-Artillery will have a small (~5%) chance of missing further from the aim-point than it used to
3. Artillery has the EXACT SAME chance to hit a target as it used to
4. Artillery will, however, miss it's aim-point by a bit more than it used to, meaning a little less splash damage on average

Hopefully this helps you better understand the 8.6 changes.

Special Thank You To wot-replays.org

In a nice little deal with WoT-Replays.org, we have expanded our collection of replays nearly five-fold to nearly 60k. That means that WoT-Replays.org will have their replays backed up for future contingencies, while we get humongous extra set of data!

Up we go!

Since we now have a model, however mediocre it may be, of tier one battles, let's extending it to add in tier two tanks. This shouldn't be too hard, tier one and tier two tanks fight each other a lot, so I went ahead and pulled a data-set of all battles featuring exclusively tier 1 and 2 tanks. That, by the way, is over 8000 battles

The first thing to look at is the Match Maker. First let's look at the distribution of numbers of tier 1s and 2s:

It's symmetric, which means I didn't mess up this time

First things to notice: There are no battles where tier 1s participate with less than 12 total tier 2s, 6 for each side. Second, it is MUCH rarer for a tier 2 tank to get into an all tier 2 battle than for tier 1s to be in all tier 1 battles, just as we would expect. Third, battles where there are more tier 2s on one side than the other don't occur infrequently, but they are rarer than equal numbers on each side (look at the odd numbers).

So, that's interesting, but what about the distribution of battles that Tier 1 tanks get? Let's count the number of Tier 2 tanks and see what we find:

I have more charts where that came from!

So, firstly, ~43% of the time a Tier 1 goes into battle, it will only see tier 1 tanks. The rest of the time at least a third of the tanks in the battle will be Tier 2 tanks. Now, as I mentioned above, the teams aren't always 'fair', in fact 26% of the time, there will be more Tier 2s on one side than the other. That's not terrible, most of it can likely be attributed to platoons.

Another interesting item I found, which at first confused me, is that Tier 2 Artillery can get into battles where all the tanks are Tier 2. In all 1308 battles where there are only tier 2 tanks present, this happened only 4 times. The obvious answer is that these are actually battle tier 3 battles which happen to be missing tier 3 tanks, but the amusing part is that it can happen.

To continue on down the road, I'm going to use the tier one model we put together last post to get a first look and see how well it matches our data. If you don't remember, this is what that model looked like:

Tank	Odds Ratio
Leichttraktor	1.0239
T1 Cunningham	1
MS-1	0.9495
Renault NC-31	0.9181
Renault FT-17	0.9096
Vickers Med. Mk. 1	0.8563

Unsurprisingly, this model doesn't perform all that great on the new data, even when limited to battles that include Tier 1s, only correctly predicting 52.2% of the the outcomes, compared to 51.6% for just choosing side 1. So, obviously, it's back to the drawing board to come with a new model, one that takes into account the new data. The model I'm going to try is going just contain the non-premium tanks, so we won't need a baseline.

Quick check to see if this makes any sense and... Hmmmm. The worst tank, by a long shot, is the Med Mk. II, a tier 2! I suppose that's not unsurprising, we've previously said that British low tiers suck. The fact that the Mk. II is actually 3% worse from the Mk. I is also highly amusing. Worse, the bottom three tanks are all British.

At the other end of the spectrum, the obvious is made evident, the 'derp' T18 dominating the low tier battles, followed by the venerable Pz. II. The difference though is quite immense,

The three 'classic' Tier 1 tanks also place higher than quite a number of tier 2 tanks. The LoLTraktor once again tops the list with the T1 and MS-1 close behind, likely due to the number of experienced players running them for fun and credits. In fact, some of the T18's power may derive from similar sources, though the 75mm seems to be the main cause.

But naturally, if we can't predict much, this isn't worth much. So, of the 8453 battles, it's important to note that this model only predicts 4658 of them, just 55.1%. The null model, just guessing a Side 1 Win, can predict 51.8%. That's an improvement sure, but not much.

At least the Trend is in the right direction

Obviously, we're showing that the choice of tank is not the biggest factor in whether a team wins. Personally, I expect we could get a lot of extra predictive power from knowing how many battles players have. It's likely that the experience of playing for a long period of time allows you to do much better against the 'noobs'. While I can't exactly vouch for a skill-based match-maker, I think that this is a perfectly good time to suggest that players with less than, say, five-hundred or a thousand battles be segregated into their own matchmaking pool for their own protection and enjoyment of the game. At least for the first couple of tiers.

For the next post I'm going to add in the low tier premiums to see if we can improve our predictive powers. Hopefully this time it won't be a week and a half between posts. After that I am going to try to tackle high tier tanks, since those are what people actually care about. By then 8.4 will likely be out and my data will be woefully out of date, so we'll go forward with obtaining more data and taking a look at how that huge 183 changed the meta game.

As always, if you enjoyed this post, please help us in our data gathering efforts. It's simple, it's easy and you can find out how just by clicking here.

A Slight Deviation for Damage Stats

Update Notice: Overlord has said that 2.5 Standard Deviations is the cut off. Edits in Bold have been added to reflect this.

As you may know, it ALWAYS feels like you're getting min-damage rolls. And the funny thing is, you're not entirely wrong. A few people have been making posts on the forums and the subreddit talking about the cause of these issues. Since the intent of this blog is to delve into the basic stats the biases of the game, I figured that this would make a good post.

If you understand the way that the Damage and Penetration (and even the aim-deviation) RNG works, it makes a lot of sense that you would see a lot more minimum damage rolls than you would expect. If you're looking for conspiracy theories, you might even think that this is done on purpose.

If you've been paying attention, you know that Damage and Penetration values vary +/-25%. If this was a uniform distribution of values, the chance of getting any damage value would entirely dependent on your mean damage. The probability of each integer damage value X would be, given a mean damage D, simply:

For a 100 damage gun? P(X) = 1.9% for any damage value between 75 and 125. A 200 penetration gun?  P(X) = 0.9% for any damage value between 150 and 250.

Now, that would seem like an easy, logical choice of a random value scheme. In fact, it's actually rather computationally "cheap", which leaves me confused by this next part:

That's not what Wargaming did. Wargaming decided that they wanted to concentrate the damage values around the average, but still provide a degree of randomization. To do this, they decided that the damage (and penetration) values should be pulled from a normal distribution, but limited to a range of 

values +/- 25% from the mean. Now, in case you don't know what a normal distribution looks like, Wikipedia provides a nice example of 3:

I certainly didn't make this, but I could have. I think.

The so-called 'Standard Normal'  (doesn't that sound redundant?) distribution is shown in red. It has a Mean of 0 and a Variance of 1. The important thing about this guy is that you can take any other normal distribution and convert it into a Standard Normal distribution with some simple calculations. Further, because of difficulty of integrating an arbitrary normal distribution, there exist standard tables of values, called Z-tables, for calculating what percentage lies under parts of the curve.

Okay, that's all well and good, but what does that tell us about are damage values? I swear I'm getting to it. One additional property about the normal distribution is important: It extends from -∞ to +∞. That means that in order to limit the variation to +/- 25% of the mean, you have to set some hard cut offs. The way Wargaming did this was to say "If we get a value below X, we'll just call it X. If we get a value about Y, we'll call it Y." What this did was to take all of the probability that was below X and give it to X and similarly take all of the probability above Y and give it to Y.

The white areas would be the probabilities rolled into Min and Max values

Now I come to a bit of a conundrum, there is a hidden parameter here that we don't know. Where we know the mean damage values for each gun, we don't know what values Wargaming has chosen for Variance (Edit: Overlord has mentioned that it is a 2.5 Standard Deviation Variance). Since Variance determines how flat or pointed the distribution is, we can't say exactly what proportion of hits should be minimum damage. However, by choosing some logical limits, we can give a good idea of what it should look like.

The obvious choices for the +/-25% limits are at the 1, 2 and 3 standard deviation lines.

Cut Off (#SDs)	% Min Value Hits
1	15.8%
1.5	6.68%
2	2.2%
2.5	0.6%
3	0.1%

Obviously, one can pull those values off the standard Z-tables. For each of these cases, we can determine the standard deviations of the distributions of based on each gun's damage. It's a pretty simple equation:

(Mean Damage)/(4*#SDs)= Damage Standard Deviation

There is one final question to be answered, how much more often do these extreme values occur than any other value? To answer this, I'm going to find the ratio of Minimum damage hits to Mean value hits. I'm going to assume that WG rounds fractions to the nearest integer, so the 'Mean' damage hits actually occur in when a value +/-0.5 from the mean is selected.

   

Gun Type	Mean Damage	1 SD	2 SD	2.5 SD	3 SD
76mm M1A1	115	11.38	0.793	0.173	0.024
88mm L/56	220	21.78	1.516	0.3315	0.0459
105mm T5E1	320	31.68	2.206	0.48	0.0668
122mm BL-9	390	38.61	2.688	0.588	0.0815
130mm S-70A	550	54.46	3.791	0.822	0.1149
155mm SA 58 AC	850	84.177	5.8589	1.27	0.1775
170mm PaK46	1050	103.9	7.237	1.579	0.219

EDIT: It has come to my attention that Overlord has clarified that the +/- 25% is a 2.5 Standard Deviation limit.

Added Damage Distribution Charts: All Y-Axis Scales are the same for easy comparison.

88mm L/56 Damage Distribution

76mm M1A1 Damage Distribution

Since the mean value is supposed to be the most likely roll, it will always be more likely than any other roll (by varying amounts). The interesting part though is the trend. As your average damage goes up, these extreme values (Min and Max rolls) increase in proportion.

If we go with the 2 Standard Deviation case , the one I find to be most likely (Particually since I remember WG saying that the aim circle was the 98% line), you'll see that a Jagdpanzer E-100 will see a min or a max damage roll 7.2 (1.58 2.5 SDs) times more often than they will see any other number! More typically armed high tier tanks will see min or max rolls 2-4 times more often (Half to 80% as often) as any other number, and all tanks with average damage greater than ~140 will see minimum and max rolls more often than average rolls.

170mm PaK46 Damage Distribution

120mm M58 Damage Distribution

Keep in mind though, for the 2 SD case, that Minimum and Maximum rolls will still only make up 4.4% of the total rolls we see. For the 2.5 SD case, they would be 1.2% of all rolls. But they are more likely than any OTHER most other specific values, especially those a bit removed from the mean, so they will seem to show up a lot (plus, how many people remember how often they hit for 159 damage? There is a bit of a confirmation bias effect going on here too).

As for Max damage rolls, there is one additional reason we see less of them than Min rolls: Low Health Tanks. When you hit a tank that has hitpoints less than your Max damage, you have a chance, dependent on their health, of wasting a roll higher than their health to kill them. If you compile all of your shots over a number of battles and don't drop kill shots, you'll find that your average damage per shot is lower than the gun's mean damage due to this effect reason.

Now, if we had a data set to help us determine the rule WG uses to truncate their random numbers, we could figure out just how badly off my assumptions are! I'll see about getting Xylenes to get some data on that...


As always, if you enjoyed this post, please help us in our data gathering efforts. It's simple, it's easy and you can find out how just by clicking here.

Technical Difficulties

To those of you who keep checking this blog, thank you very much. I hope to have a new analysis up in the next couple of days, but I have been having some computer issues, so it's taking much long than expected. Thanks for your patience and support.

Yea, but how important is it?

Over the last few posts, I've been providing you with a look at battles on Province, the crazy low-tier map that's so unbalanced it makes your head hurt. With that look, I gave you a list of tanks and a number that represented how they affect your win chances if you plugged your team composition into a fancy formula.

Today I'm going to take a step back and try to inform you something about their usefulness: how well do they let us predict the outcome of battles?

I do this for two reasons:

1. The only way to know if these numbers mean anything is to apply them to data and see if you get accurate predictions.
2. People who know their statistics keep harping on me to do some legit hypothesis testing/other statistical things.

So, to evaluate how good my regressions are, I'm going to slip off into a slightly different data set: All Tier 1 Battles. 1576 battles were included in the model generation, another 1506 in the validation set (these were separated randomly). Again, T1 Cunninghams were used as the baseline tank.

Once again we see an interesting distribution, ~51% of games are won by side 1, however we can attribute it to:

A. Effects of Province on the total distribution.
B. Random chance.

We know A from the last set of analyses, while we know B from the P-value of the intercept, at a 28.9% chance of getting that value purely by chance, we can't reject the null hypothesis of battles being, on average, 50/50. So, I'm going to run it again, forcing this value:

This obviously isn't much of a difference, but it will give us a good starting point. In summary, from best to worst:

Tank	Odds Ratio
Leichttraktor	1.09
MS-1	1.019
T1 Cunningham	1
Renault NC-31	0.965
Renault FT-17	0.915
Vickers Med. Mk. 1	0.901

Hey look, I made a table! But I've stuck something in here that you probably haven't seen before, the Odds Ratio. It's really not hard to understand, it's just the amount that your base odds (in this case 0.5, or 50%) is multiplied by for each unit increase in that variable.

Example Battle: Somebody got Annihilated!

Count 'em up: Even LTraktors, Even FTs, Side 1 has +1 MK. I, Side 2 has +1 MS-1, Even T1s. So to predict the outcome is pretty simple:

Overall Odds Ratio = (1.09)⁰•(1.019)^-1•(0.965)⁰•(0.915)⁰•(0.901)¹= 0.882 or ~9:10 odds

And since P = (Odds)/(Odds + 1):

46.86% Win Chance

Obviously this isn't the best of odds for our eventual winners, so lets see how well it does on other data.

If we were to just choose side 1 to win the entire time, we would get it right ~50% of the time, 51.4% in the case of this data. How well does the model predict it? Well, if we compare it to the data we used to generate the model, it gets 735 cases wrong (By wrong, I mean it gave side 1 a >50% chance of winning but side 2 won, or vice-versa). Remember that we had a total of 1576 battles, so our error rate with this model is 46.6%. In other word, this model only predicts 2% more battles correctly than you would if you laid your money all on one side, 3.4% than if battles are truly balanced. That may be good enough for Vegas odds makers, but not that great for us.

Applying it to the test set, the results aren't particularly good either. In fact, if we apply this data to my test set of 1506 battle, it only get 50.6% right! That's terrible! Scarcely better than flipping a coin! Surely there has to be some way we can make it better?

Well the first thing to do is combine the two data sets. Stick them together and what do you get?

On this one I forced a 50% Win Rate

But not on this one.

From these you can clearly see that doubling the amount of data definitely increased the significance of each of the coefficients except for the LoLTraktor. Further the difference between these two models is pretty small, which is a sign of stability in the outcomes. The intercept shows that 52% of all battles are won by side 1, but now the significance level is such that we're mostly left with option A for an explanation. But now we get a whole new set of Odds Ratios:

Tank	50% Model	52% Model
Leichttraktor	1.0268	1.0239
T1 Cunningham	1	1
MS-1	0.9516	0.9495
Renault NC-31	0.9179	0.9181
Renault FT-17	0.9106	0.9096
Vickers Med. Mk. 1	0.8583	0.8563

Looking at it this way we can see a new shift in the data, suddenly the MS-1 drops below the T1. But we still need to do the important part, see how well the model predicts.

So, of the total 3082 tier 1 battle, the previous model, based on half the data, had only predicted 1603 right, a tepid 52%. With these new models, we should see some drastic improvement, right?


Behold! The mighty power of the 50% Model! 1550 Correct predictions! An astounding 50.3%! Wait, that's actually WORSE than having no predictors at all! It's scarcely even an improvement on our 50/50 win split assumption! That's terrible!  Maybe the other model will do better...

The power of the 52% Model will astonish you with 1666 correct predictions! 54.05% correct! That's right, 60 more correct predictions! 2% additional accuracy! The slivers of probability that gambling careers are made of. But still not a tool you'd want to bet the house on. Obviously there's more to these battles than tank type.


So basically, the moral of the story is this: At least down here, at tier 1, the differences in tanks are so small that building a prediction tool based soley on tank types isn't going to help you much. No tank is so overpowered that it overrides skill or luck in determining the outcome of the match. rather the differences in tanks is just as likely to be a bias in the players who favor them, which is something we'll have to control for at some point.

As always, if you enjoyed this post, please help us in our data gathering efforts. It's simple, it's easy and you can find out how just by clicking here.

And the Winner is...

At this point I've probably bored you enough with my forays into telling you which tiers and nations are better on one weee 'ittle map visited only by tier 3 and under tanks. But I have one last big reveal, the full listing. Trying to estimate just how good all 54 tier 3 or less tanks are on Province represents a lot of typing, after all, those names are long, but for you, I did it.

Now, to get you ready, I used as my baseline the T1 Cunningham, so positive values indicate it's better to have that tank than a Cunningham, while negative values indicate you're better off with the Cunningham.

Honestly, I rather surprised by just how many of these produce significant results. If you read the previous posts, you'll notice that most of these values fall in line with the findings from their regressions: Artillery is bad, TDs good, Premium Tanks good. The two best tanks to have on your team are German Premiums. Tier 1&2 British tanks are poor shadows of their counterparts.
The best:

PzKpfw II Ausf J: This one really surprises me, since looking through the data I can only find one instance of it appearing in a battle. But the data suggests (with a surprising level of significance) that having one on your side gives you a nearly 30% increase in win chance. Obviously either the tank or those who drive it are extremely good...

PzKpfw S35: Another tier 3 German premium, this one give you an extra ~25% chance of winning compared to having a Cunningham.

M22 Locust: American Premium this time, boasting a respectable +23% win chance.

FCM36 PaK40: The French Tier 3 TD seems almost perfect for this map, long view range and powerful gun. It's slowness is not a problem as there isn't much movement to do. This translates to a +22% win chance.

PzKpfw 38H735.f: The infamous Micro-Maus gets the distinction of being the only Tier 2 to make the top 5. Each one on your side give +21% chance of winning.


Obviously it's easy to find a pattern to this data. Premiums are good, Artillery Bad, the lower the tier the worse the tank. It's pretty simple to understand why this is, most people don't play the Tier 1-3 for more than a couple weeks, and even then, rarely with elited tanks and good crews. Premium tank players on the other hand tend to have more experience and are willing to pay, both gold and credits, for better crews and ammo. Further, premiums have no XP grind, so you're never going to find a premium tank fighting at less that full effect.

In an attempt to verify this theory, let us take a look at two premium tanks in particular, the T1E6, this year's gift tank and the M3 Light, the Lend-Lease M3 Stuart that players could get by finishing the tutorial. One peculiarity of the M3 Light is that when you get it, it comes with a free 100% crew, giving players with little experience a fully qualified crew much sooner than they would hav otherwise.

The T1E6, on the other hand, was gifted to everyone with a 50% crew. If you were like me, you immediately dismissed them to place your trained Chaffee crew members in it. But some people forget that it is a premium tank and can use tankers trained on other vehicles.

Comparing the M3 and the T1E6, it's fairly obvious that the M3 underperforms for it's tier, the fact that  50% crew tier 2 and a 100% crew tier 3 perform similarly is ample evidence of that. Comparing to other tier 3 premiums, the skill differential can be estimated at about 0.8, or 16% win chance. This shows that experience is not an irrelevant factor, but having a good crew is also important.


One thing you may have noticed is that the map bias we noted in the last two post is a bit higher in the full tank run. Also, we have some rather extreme biases toward high skill players in the form of premium tanks. How about we try to cut out that bias by removing the premium tanks.

Ok, I messed up a little. The T1E6 stayed in and I don't access to my regression currently to fix it. But, other than a few top tier tanks, almost every tank was close to 5% significance level. And all the low tier ones were highly significant. Plus the map bias has tweaked a bit down toward where we've had it previously.

One thing that should pop out immediately is that almost all of these tanks have negative coefficents, the M3 Stuart being the sole exception (With about 45 predictors, it's rather amazing that we only had one that truely deviated. Further, the significance level indicates just how random that value truely is, so I am going to ignore it and wait for more data). This tells me that it's not so much a question of who is better, but of who is less bad. Obvious offenders appear again, Artillery tends to be close to -0.9, some TDs are very good, others not quite so good.

The surprise winner among these tanks? The French D2 Medium, though it too is a low significance result. Beyond that, the Chi Ha and Luchs make good showings. The most surprising tank would be the classic LoLTracktor (Leichttraktor) which performs 0.11 points better than it's fellow tier ones, though this may be attributed to nostolgia driving by high skill players.

One could make a whole chart of which tanks are good, bad and balanced. But I will leave that for another time.




As always, if you enjoyed this post, please take a moment and download our Replay Upload Tool. It's simple and fast to use and each replay improves the quality of our data and the results we can show!